크루스칼 알고리즘
크루스칼 알고리즘(Kruskal's algorithm)은 최소 비용 걸침 나무를 찾는 알고리즘이다. 간선의 개수를  , 점의 개수를
, 점의 개수를 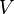 라고 하면 이 알고리즘은
라고 하면 이 알고리즘은  의 시간복잡도를 가진다.
의 시간복잡도를 가진다.
목차[숨기기] |
[편집] 개요
크루스칼 알고리즘은 아래의 순서대로 작동한다.
- 그래프의 각 정점이 각각 하나의 트리가 되도록 하는 포레스트 F을 만든다.
- 모든 간선을 원소로 갖는 집합 S를 만든다.
- S가 비어있지 않는 동안
- 가장 작은 가중치의 간선을 S에서 하나 빼낸다.
- 그 간선이 어떤 두 개의 트리를 연결한다면 두 트리를 연결하여 하나의 트리로 만든다.
- 그렇지 않다면 그 간선은 버린다.
알고리즘이 종료됐을 때 포레스트 F는 하나의 최소 비용 걸침 나무만을 가지게 된다.
[편집] 시간 복잡도
 를 간선(edge)의 개수라 하고,
를 간선(edge)의 개수라 하고, 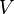 를 정점(vertice)의 개수라고 하자. 크루스칼 알고리즘은
를 정점(vertice)의 개수라고 하자. 크루스칼 알고리즘은  시간 안에 동작한다고 증명될 수 있다. 간단한 자료 구조가 쓰인다면
시간 안에 동작한다고 증명될 수 있다. 간단한 자료 구조가 쓰인다면  안에 동작한다. 이 동작 시간은 동일한데, 그 까닭은 다음과 같다:
안에 동작한다. 이 동작 시간은 동일한데, 그 까닭은 다음과 같다:
 는 최대
는 최대  개일 수 있다.
개일 수 있다.  는
는  이다.
이다.- 홀로 떨어진 정점(vertices)들을 무시한다면 (그들 각각은 그만의 최소 비용 걸침 나무가 된다.),
 이다. 그러므로
이다. 그러므로  는
는  이다.
이다.
이러한 시간 복잡도 한계는 다음과 같은 방법으로 도달할 수 있다.: 간선(edge)들을 그들의 무게(weight) 순으로  시간 내에 정렬한다; 정렬을 함으로써, "집합 S로부터 최소 무게(weight)를 갖는 간선(edge)를 제거한다"는 동작이 상수(constant) 시간에 행해질 수 있게 된다. 디스조인트-셋 자료 구조(유니온 파인드: 결합과 검색)를 이용하여 어떤 정점(vertice)이 어떤 콤포넌트(component)에 속하는 지 추적한다. 디스조인트-셋 찾기(find) 동작 두 번에
시간 내에 정렬한다; 정렬을 함으로써, "집합 S로부터 최소 무게(weight)를 갖는 간선(edge)를 제거한다"는 동작이 상수(constant) 시간에 행해질 수 있게 된다. 디스조인트-셋 자료 구조(유니온 파인드: 결합과 검색)를 이용하여 어떤 정점(vertice)이 어떤 콤포넌트(component)에 속하는 지 추적한다. 디스조인트-셋 찾기(find) 동작 두 번에  시간이 걸린다. 각 간선(edge)이 각각 한 유니언(union) 안에 있다고 가정하면 말이다. 간단한 디스조인트-셋 자료 구조인 랭크에 의한 합집합을 사용하는 디스조인트-셋 포레스트(disjoint-set forest with union by rank)를 쓰더라도,
시간이 걸린다. 각 간선(edge)이 각각 한 유니언(union) 안에 있다고 가정하면 말이다. 간단한 디스조인트-셋 자료 구조인 랭크에 의한 합집합을 사용하는 디스조인트-셋 포레스트(disjoint-set forest with union by rank)를 쓰더라도,  개의 동작이
개의 동작이  시간 안에 행해진다. 그러므로 총 시간 복잡도는
시간 안에 행해진다. 그러므로 총 시간 복잡도는  가 된다.
가 된다.
간선(edge)들이 이미 정렬되어 있거나 선형 시간(linear time,  ) 안에 소트될 수 있다면(예를 들어 카운팅 정렬, 라딕스 정렬), 크루스칼 알고리즘은 좀 더 고도의 디스조인트-셋 자료 구조를 사용할 수 있다. 이때 동작 시간 복잡도는
) 안에 소트될 수 있다면(예를 들어 카운팅 정렬, 라딕스 정렬), 크루스칼 알고리즘은 좀 더 고도의 디스조인트-셋 자료 구조를 사용할 수 있다. 이때 동작 시간 복잡도는  가 되는데, 여기서
가 되는데, 여기서  는 아주 느리게 증가하는 단일-값 애커만 함수의 역함수를 말한다.
는 아주 느리게 증가하는 단일-값 애커만 함수의 역함수를 말한다.
[편집] 예제
 |
우리가 풀어야 할 그래프이다. 간선(arc) 옆에 있는 숫자는 간선의 무게(weight)를 가리킨다. 지금은 모든 간선(arc)들이 색이 동일하다. |
 |
AD 와 CE 가 가장 짧은(weight가 가장 작은) 간선이다. 아무거나 골라서 AD를 선택한다. AD의 색을 변경하였다. |
 |
이제, CE가, 무게(weight)가 5로서, 루프(loop)를 생성하지 않는 가장 짧은 간선이다. CE의 색을 변경하였다. |
 |
같은 방식으로 고르면 다음 간선은 DF이다. 무게(weight)는 6이다. |
 |
다음으로 가장 짧은 간선은 AB와 BE인데, 둘 다 길이 (= 무게(weight))가 7이다. 임의로AB를 골랐다. BD는 빨강색으로 변경하였는데, ABD를 연결시키면 루프를 이루기 때문이다. |
 |
다음으로 가장 짧은 간선은 BE로서 길이 7이다. 더 많은 간선들이 빨강으로 변했다. BCE 루프를 생성하기 때문에 BC가 빨강색으로 변했으며, DEBA 루프를 생성하기 때문에 DE가 빨강색으로 변했고, |
 |
끝내, EG가 연결되면서 알고리즘이 종료된다. 최소 비용 걸침 나무가 완성되었다. |
[편집] 정확성 증명
 를 정점들이 연결된(connected) 무게 값이 있는(weighted) 그래프라고 가정하자. 또한
를 정점들이 연결된(connected) 무게 값이 있는(weighted) 그래프라고 가정하자. 또한  를 크루스칼의 알고리즘을 써서 만들어낸
를 크루스칼의 알고리즘을 써서 만들어낸  의 서브그래프라고 가정하자.
의 서브그래프라고 가정하자.  는 순환고리(cycle)를 가질 수 없다. 마지막 간선(edge)이 하나 추가되어 순환고리를 생성한 것이라면, 그 마지막 간선(edge)은 서로 다른 트리 사이에 존재할 수 없으며, 한 서브트리 내에 존재해야만 하기 때문이다. (순환고리를 만들려면 각 정점들이 한 서브트리 내에서 이미 이어져 있어야 한다. 알고리즘의 절차상 그러한 마지막 간선(edge)을 만들 수 없다는 뜻이다.)
는 순환고리(cycle)를 가질 수 없다. 마지막 간선(edge)이 하나 추가되어 순환고리를 생성한 것이라면, 그 마지막 간선(edge)은 서로 다른 트리 사이에 존재할 수 없으며, 한 서브트리 내에 존재해야만 하기 때문이다. (순환고리를 만들려면 각 정점들이 한 서브트리 내에서 이미 이어져 있어야 한다. 알고리즘의 절차상 그러한 마지막 간선(edge)을 만들 수 없다는 뜻이다.)  는 연결 안 된(disconnected) 그래프일 수가 없다.
는 연결 안 된(disconnected) 그래프일 수가 없다.  내에 연결 안 된 콤포넌트가 있었다면, 알고리즘의 절차에 의해, 그 둘을 연결하는 간선(edge)이 추가되었을 것이기 때문이다. 결론을 내리면,
내에 연결 안 된 콤포넌트가 있었다면, 알고리즘의 절차에 의해, 그 둘을 연결하는 간선(edge)이 추가되었을 것이기 때문이다. 결론을 내리면,  는
는  의 스패닝 트리이다.
의 스패닝 트리이다.
다음으로는 스패닝 트리  가 미니멈 스패닝 트리임을 보이겠다.
가 미니멈 스패닝 트리임을 보이겠다.
 이 미니멈 스패닝 트리라고 가정하자. 만약
이 미니멈 스패닝 트리라고 가정하자. 만약  이면
이면  도 미니멈 스패닝 트리가 된다. 이게 사실이 아니라고 가정하자.
도 미니멈 스패닝 트리가 된다. 이게 사실이 아니라고 가정하자.  가
가  에는 있으나
에는 있으나  에는 없는 간선(edge)이라고 가정하자.
에는 없는 간선(edge)이라고 가정하자.  는 순환고리(cycle)을 가질 수밖에 없다. 스패닝 트리에 간선을 하나 더하면 더 이상 스패닝 트리가 아니기 때문이다. 이 순환고리(cycle)는 다른 하나의 간선(edge)
는 순환고리(cycle)을 가질 수밖에 없다. 스패닝 트리에 간선을 하나 더하면 더 이상 스패닝 트리가 아니기 때문이다. 이 순환고리(cycle)는 다른 하나의 간선(edge)  를 가지는데,
를 가지는데,  는
는  가
가  에 추가되는 알고리즘의 단계에서 고려 안 된 간선(edge)일 수밖에 없다. 안 그랬다면
에 추가되는 알고리즘의 단계에서 고려 안 된 간선(edge)일 수밖에 없다. 안 그랬다면  는 같은 트리의 다른 브랜치(branch)들을 서로 연결했을 것이고, 서로 다른 트리들은 연결시키지 않았을 것이기 때문이다. 그러므로
는 같은 트리의 다른 브랜치(branch)들을 서로 연결했을 것이고, 서로 다른 트리들은 연결시키지 않았을 것이기 때문이다. 그러므로 도 역시 스패닝 트리이다. 이 스패닝 트리의 총 무게 합(total weight)은
도 역시 스패닝 트리이다. 이 스패닝 트리의 총 무게 합(total weight)은  의 총 무게 합(total weight)보다 작다. 그 까닭은
의 총 무게 합(total weight)보다 작다. 그 까닭은  이므로 알고리즘이
이므로 알고리즘이  를 방문하기 전에
를 방문하기 전에  를 먼저 방문했기 때문일 것이다. 만약 무게값(weight)들이 같았다면, 우리는
를 먼저 방문했기 때문일 것이다. 만약 무게값(weight)들이 같았다면, 우리는  에는 있으나
에는 있으나  에는 없는 간선(edge)
에는 없는 간선(edge)  를 생각할 수 있다. 만약 남아 있는 간선(edge)이 없었다면,
를 생각할 수 있다. 만약 남아 있는 간선(edge)이 없었다면,  나
나  가 서로 다른 간선(edge)들로 구성되어 있었더라도
가 서로 다른 간선(edge)들로 구성되어 있었더라도  의 총 무게 합이
의 총 무게 합이  의 총 무게 합과 같을 것이다. 이 때도 역시
의 총 무게 합과 같을 것이다. 이 때도 역시  는 미니멈 스패닝 트리가 된다. 만약
는 미니멈 스패닝 트리가 된다. 만약  의 총 무게 합이
의 총 무게 합이  의 총 무게 합보다 작은 경우에는,
의 총 무게 합보다 작은 경우에는,  이 미니멈 스패닝 트리가 아니라는 결론에 다다르게 된다. 이것은
이 미니멈 스패닝 트리가 아니라는 결론에 다다르게 된다. 이것은  인 간선(edge)
인 간선(edge)  가 있다는 처음의 가정에 위배되게 된다. 결론적으로,
가 있다는 처음의 가정에 위배되게 된다. 결론적으로,  는 (
는 ( 과 간선들도 같고, 무게도 같은) 완전한 미니멈 스패닝 트리가 될 수밖에 없다.
과 간선들도 같고, 무게도 같은) 완전한 미니멈 스패닝 트리가 될 수밖에 없다.
[편집] 의사 코드
1 function Kruskal(G)
2 for each vertex v in G do
3 Define an elementary cluster C(v) ← {v}.
4 Initialize a priority queue Q to contain all edges in G, using the weights as keys.
5 Define a tree T ← Ø //T will ultimately contain the edges of the MST
6 // n is total number of vertices
7 while T has fewer than n-1 edges do
8 // edge u,v is the minimum weighted route from/to v
9 (u,v) ← Q.removeMin()
10 // prevent cycles in T. add u,v only if T does not already contain an edge consisting of u and v.
11 // Note that the cluster contains more than one vertex only if an edge containing a pair of
12 // the vertices has been added to the tree.
13 Let C(v) be the cluster containing v, and let C(u) be the cluster containing u.
14 if C(v) ≠ C(u) then
15 Add edge (v,u) to T.
16 Merge C(v) and C(u) into one cluster, that is, union C(v) and C(u).
17 return tree T
[편집] 참고 문헌
- Joseph. B. Kruskal: On the Shortest Spanning Subtree of a Graph and the Traveling Salesman Problem. In: Proceedings of the American Mathematical Society, Vol 7, No. 1 (Feb, 1956), pp. 48–50
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 23.2: The algorithms of Kruskal and Prim, pp.567–574.
- Michael T. Goodrich and Roberto Tamassia. Data Structures and Algorithms in Java, Fourth Edition. John Wiley & Sons, Inc., 2006. ISBN 0-471-73884-0. Section 13.7.1: Kruskal's Algorithm, pp.632.
[편집] 같이 보기
[편집] 바깥 고리
'Network Flow Algorithm' 카테고리의 다른 글
| [펌]Maximum Flow Algorith 1 (0) | 2012.09.13 |
|---|---|
| Sollin algorithm (0) | 2012.09.11 |
| [펌] Prim's algorithm (0) | 2012.09.11 |
| [펌]Kruskal's algorithm (0) | 2012.09.11 |
| [펌] Prim's algorithm - Wiki (0) | 2012.09.11 |
